@[toc]

动态规划-Introduction

1.了解动态规划

灵活: 动态规划题目中类型丰富,套路代码较少,专杀"过拟合的神经网络"们!

质量: 问题中的阶段划分,状态设计,状态之间转移以及一些边界都是需要自己思考的

简单: 代码质量不高,想到合适的思路后可以快速实现,字里行间都能体现出水平

2.基本术语

1.基本概念,统一一下术语.

• 动态规划:运筹学中的一个分支,是求解决策过程最优化的数学方法.
• 阶段:把所给求解问题的过程恰当地分成若干个相互联系的阶段.
• 状态:状态表示每个阶段开始面临的自然状况或客观条件

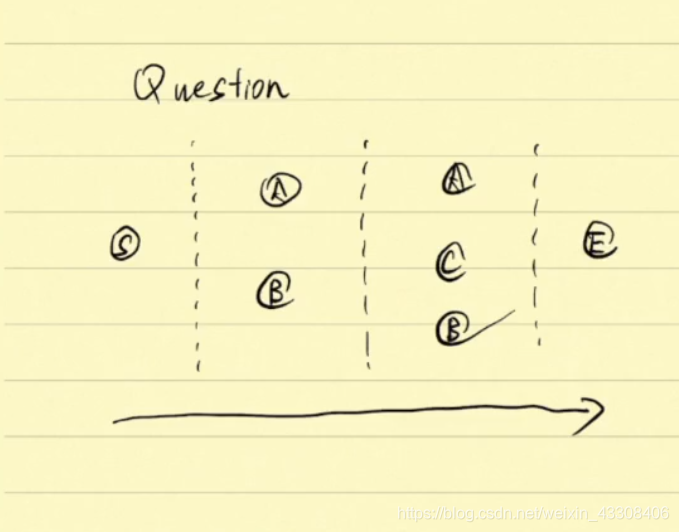
• 决策(转移):一个阶段的状态给定以后,从该状态演变到下一个阶段某个状态的一种选择成为决策.
• 策略:每个阶段都要做一个决策,一系列决策的集合.
• 边界: 初始集合.

2.动态规划的状态设计

其实包含两步：阶段划分与状态设计，这两部分的关系又非常紧密，所以面对问题的时候放在一起思考，统称为状态设计。简单来说，我们把原问题划分成若干个不相交的部分，这每一个部分就是一个阶段，而具体看每一个阶段的时候，需要一些信息来刻画阶段中不同的情况。不同的情况就是状态，刻画情况的信息就是状态的表示。

这样看上去，阶段和状态似乎没有什么区别，都是用来描述问题不同情况的。这时候就需要决策上场了。决策，对应动态规划中的状态转移，一个决策可以从一个阶段的状态演变到另一个 不同 阶段的状态中去，如果将阶段看成是点，决策看成是连在阶段间的有向边，那么这两个东西一定组成的是一个 DAG（有向无环图）。这也是保证了动态规划问题的优秀复杂度，即同一个状态不会直接 / 间接的更新自己。

这样说起来，很是抽象，我们举一个简单的例子，并用动态规划的方法来分析这件事情。 吃完饭，WNJXYK 想要和 VineAsh 一起去看电影。那么他要处理几个问题：

• 电影票：他可以出发前网上订票 / 到电影院现场买票
• 清洁餐具：出发前洗碗 / 看电影后回家洗碗

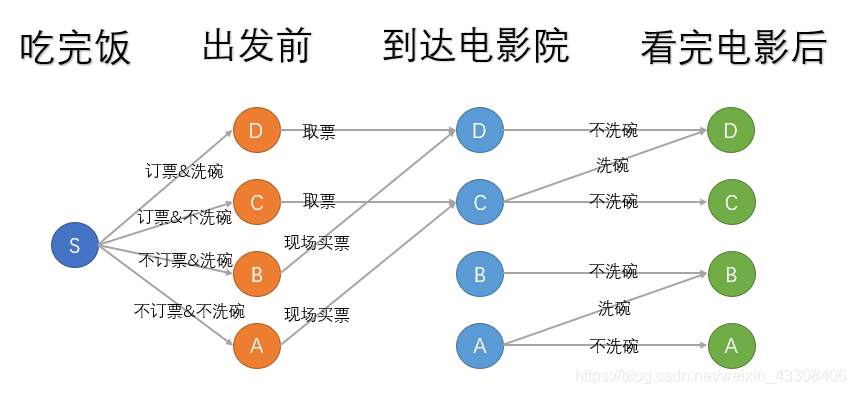
1.寻找划分阶段,也就是上图中的几个标题大字.

2.来分析状态,也就是上图中的圆圈.

3.确定状态转移,也就是连接圆圈之间的有向箭头.

4.初始状态 也就是状态 S，这个也是由问题确定的。

3.动态规划问题性质

1.三个动态规划需要满足的性质

接下来，我们了解三个动态规划状态需要满足的性质：

• 最优子结构：一个最优化策略的子策略总是最优的，反过来，我们可以通过最优的子策略，推出最优策略。
• 无后效性：当我们通过一系列策略到达了某一阶段的某一状态时，下一步决策不受之前的一系列策略影响，仅由当前状态决定。
• 子问题重叠：算法计算的过程中会反复地求解相同的一定量的子问题，而不是不断生成没有见过的新问题。也就是说子问题空间不大，或是状态空间不大，我们可以通过存储状态的答案加快计算速度。

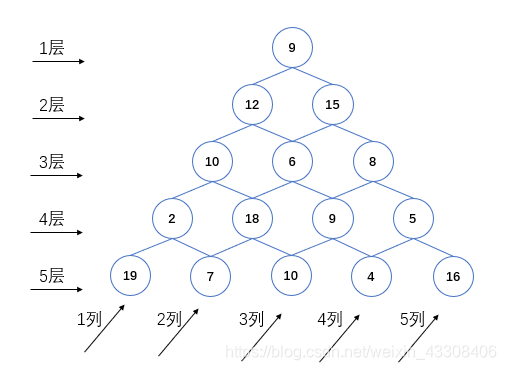
eg: 拿动态规划的经典问题数塔来举例子：有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

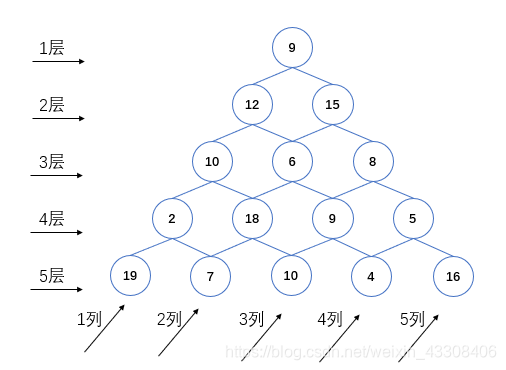
首先考虑上一节所说的状态表示与转移，我们先找一组符合动态规划要求性质的表示与转移：

• 阶段：数塔的每一层就是一个阶段，转移的时候，从上一层向下一层转移。
• 状态：位于数塔每一层的那个节点就是状态，因为每一步只能走到相邻的节点，所以状态决定了能够向下一阶段的哪些状态转移。
• 状态转移：由题目中 每一步只能走到相邻的结点得到，状态转移就是上一层节点向下一层相邻节点转移。
• 初始状态：由题目中得到，数塔顶部节点。

如此，我们的可以由阶段和状态得到：

• 状态表示：dp[i] [j]表示位于第 i 层第 j 个元素的最大数字之和
• 状态转移即为 dp[i] [j] = max(dp[i-1] [j-1], dp[i-1] [j]) + v[i] [j]
• 初始状态为 dp[1] [1] = 9。

对照着性质一条一条看，分析以下动态规划的性质：

如果我们当前在状态 (i,j)（即第 i 行第 j 列，下同），我们只能从状态 (i−1,j−1) 与状态 (i−1,j) 走过来,(i,j) 的最优决策一定能由它的两个子决策 (i−1,j−1) 与 (i−1,j) 推导出来，这就满足了最优子结构性质。反应到状态转移方程中，我们就可以放心的令 dp[i] [j] = max(dp[i-1] [j-1], dp[i-1] [j]) + v[i] [j]。（因为不关系具体决策序列，只关心结果，我们将最优决策得到的数字之和存储与 dpd**p 数组中）

当我们在状态 (i,j) 的时候，我们考虑状态 (i−1,j−1) 或状态 (i−1,j) 走过来，无需在多考虑之前是怎么走到(i−1,j−1) 或是(i−1,j−1) 的，这就是无后效性。其实，后效性这东西和状态表示是密切相关的，如果你发现你的状态表示存在后效性，那么把没考虑的东西加入状态表示中去，那么这个后效性的就消除了。解决动态规划问题的时候，我们需要寻找一个满足无后效性的最简状态表示。

整个问题的子问题其实只有 n(n+1)/2 种，子问题空间有限，是 O(n^2) 级别的。

2.反面教材(不满足性质)

然后，我们看两种反面教材：

状态表示为 dp[i] 表示位于第 i 层的最大数字之和，这种状态表示具有后效性，因为我们从上层往下层转移的时候，因为受到题中移动的相邻节点限制且状态中不知道相邻信息，没办法直接通过 dp[i−1] 转移到 dp[i]。我们需要多记录一维层内位置来消除后效性。

状态表示为 dp[a,b,c,d,e] 第一层走节点 a，第二层走节点 b，……，第五层走节点 e 的最大数字和。状态唯一的表示了每一种数塔行走的情况，不存在子问题重叠了，这样子问题数量增加至 n!，无法接受。

将题目更改为求从上向下的数字路径上的最大值最小值之差，那么使用 dp[i] [j]表示走到第 i 层第 j 个元素的最大值最小值之差就不符合最优子结构了，即使(i,j)，只能从状态 (i−1,j−1) 与状态(i−1,j) 走过来且 (i−1,j−1) 与(i−1,j) 最优，我们也无法通过 (i−1,j−1) 与 (i−1,j) 的结果推出(i,j) 的最优决策，想想这是为什么~

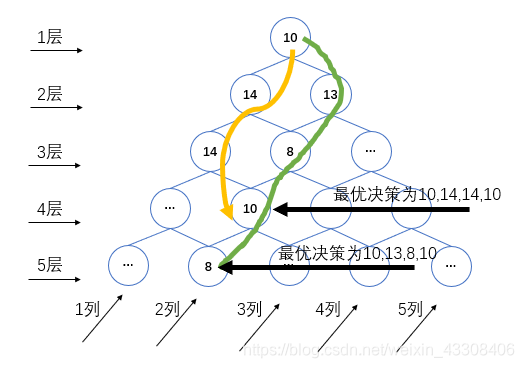
假设下图的情形，我们不考虑其他节点的值（假设其他都不是最优的），对于状态 (4,2)(4,2)，两种路径：[10, 14, 14, 10] 的差为 4，[10, 13, 8, 10]的标准差为 55，显然最优决策为橙色箭头标识。状态 (5,2)(5,2) 的数字为 8，从 (4,2)(4,2) 的最优决策 [10, 14, 14, 10转移过来，显然不如从非最优决策 4，[10, 13, 8, 10] 转移。（[10, 14, 14, 10, 8] 差为 6，[10, 13, 8, 10, 8] 差为 5）此状态的最优策略并非从子最优决策推得，反而是从非最优子决策得到的，这就是不符合最优子结构性质。

一般来说，求最大值、最小值这种目标式单调的问题，最优子结构性质是符合的，求什么绝对值、标准差、差值之类的，前期结果雪崩，到最后一步力挽狂澜的问题，最优子结构不能符合。

4.动态规划 题目特点

动态规划原本是用来解决求最值这类的最优化问题的，后人将其原理直接应用于计数、存在性判定（本质上也是计数）一类的问题也能够 work，所以如果你看到最值、计数(满足什么要求的方案数是多少?)、存在性判定(满足这个的方案存不存在?)这三类问题，不妨思考一下使用动态规划来解决。

再看数塔问题，同样要求从顶层走到底层，若每一步只能走到相邻的结点，最值就是求走出一条路径的最大数字和是多少，计数可以是求走出一条路径数字和不超过 55 的方案数，存在性判定可以是求是否存在一条路径的数字和等于 55。

5.动态规划代码实现

两种写代码的方式：记忆化搜索与递推。我认为记忆化搜索是一种相对容易理解好上手的代码方式，递推需要考虑更多的东西，优点是支持加入各种高级优化。

1.记忆化搜索

先说记忆化搜索，我认为这是一个相对简单的动态规划实现方法。它可以理解为在我们确定的状态上进行搜索，然后通过一个额外的数组保存每一个状态的答案，搜索某一个状态时，如果答案计算过就直接返回，否则继续向下搜索并保存计算过的答案！所以，点了搜索技能点的同学可以快速转型到记忆化搜索，它的好处有以下几点：

• 能避免计算一些根本用不到的状态。
• 决策边界容易考虑，搜不下去就是边界。
• 减少思考量，不用考虑状态之间的计算顺序，程序只需要立足当前状态与当前状态的子状态即可。
• 实现容易，写出搜索，加个记忆化就完事了。
• 可以使用搜索的奇技淫巧优化。

因为记忆化搜索存在一个搜索的框架，所以可以写出一个比较抽象的模板：

int dp[状态表示];
public int dfs(状态表示){
    if (决策边界) return 决策边界;//决策边界
    if (dp[状态表示] != 无效数值) return dp[状态表示];// 记忆化
    for (当前状态表示的 子状态) dfs(子状态) 更新 dp[状态表示];//状态转移
    return dp[状态表示];
}
public int slove(){
    return dfs(原问题状态);
}

2.递推

再讲递推，简单了说是使用 For 循环嵌套对所有状态进行枚举，使用转移方程更新状态。

这里枚举状态的顺序就有讲究了，比如我们更新状态 A，需要状态 B、C、D 的答案，那么状态 B、C、D 肯定要先于状态 A 被我们枚举到，换句话说，确定状态 A 的时候，状态 B、C、D 必须已经被确定完了。一般来说，我们按照阶段地顺序枚举状态就可以了，但是很多时候问题情况比较复杂，按照阶段未必时最简单最容易实现的方法，所以枚举状态的顺序需要仔细思考。虽然，递推的实现方法相对记忆化搜索困难，但是他也有优点：

• 可以加入各种动态规划优化
• 没有记忆化搜索中系统栈的开销，速度较快

6.动态规划解答例题

动态规划的核心就是状态表示，我们要确定一个既不是那么复杂导致超时，又不过于简单产生后效性的合理状态表示。有了一个合理的状态表示之后，转移方程、决策边界和代码实现都是稍加思考就能得到了。

Step 1 确定状态表示，包含阶段划分与状态表示 Step 2 写出转移方程：帮助你想清楚状态之间到底是如何转移的 Step 3 确定边界：初始 Cases！ Step 4 如果使用递推，考虑一下子状态枚举的顺序。

另外，一件重要的事情是：想清楚了再写代码、想清楚了再写代码、想清楚了再写代码！

做道例题：64. 最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

先确定状态表示，这道题目里的阶段比较隐式，它是斜过来在对角线上的元素。想想为什么，阶段 1 是从距离起点 0 步的位置，阶段 2 是距离起点 1 步的位置……我们总是从上一个阶段的状态向下一个阶段的状态进行更新。

那么，在每一个阶段中，我们需要知道它的具体位置，即斜线上的第几个，我们可以令 dp[i][j]表示在阶段 i 位于从上向下第 j 个的最小路径和。这样定义状态是可以将此题做出来的，但是会带来很多实现上的麻烦。 我们也可以令 dp[i][j]表示位于网格第 i 行第 j 列的最小路径和，这样阶段等于i+j，依旧能隐式地表示阶段。、

状态转移方程，由题目中 每次只能向下或者向右移动一步 这句话得到，也就是 (i,j) 可以从 (i−1,j) 与 (i,j−1) 走过来，那么转移方程就是 dp[i] [j] = min(dp[i-1] [j], dp[i] [j-1]) + grid[i] [j]。

决策边界，棋盘只有一个起点，所以 dp[0] [0] = grid[0] [0]。如果超出棋盘，也是不行的。

1.记忆化搜索的代码

class Solution {
    public int minPathSum(int[][] grid) {
        //行边长度：
        int m = grid.length;
        //纵边长度：
        int n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[0][0] = grid[0][0];
        //初始化：
        for(int i = 1;i<m;i++){
            dp[i][0] = dp[i-1][0]+grid[i][0];
        }
        for(int j=1;j<n;j++){
            dp[0][j] = dp[0][j-1]+grid[0][j];
        }
        //转义方程：
        for(int i  =1;i<m;i++){
            for(int j =1;j<n;j++){
                dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1])+grid[i][j];
            }
        }
        return dp[m-1][n-1];
    }
}    
//3ms

class Solution {
    public int minPathSum(int[][] grid) {
        if(grid.length == 0) return 0;
        int m = grid[0].length, n = grid.length;
        return minPathSumDfs(m, n, new int[n][m], grid);
    }

    private int minPathSumDfs(int m, int n, int[][] cache, int[][] grid){
        // 搜不下去就是边界
        if(m == 1 && n == 1) return grid[n - 1][m - 1];
        if(m < 1 || n < 1) return Integer.MAX_VALUE;
        
        // 记忆化
        if(cache[n-1][m-1] != 0 ) return cache[n-1][m-1] - 1;
        
        // 状态转移
        int sum = Math.min(minPathSumDfs(m - 1, n, cache, grid), minPathSumDfs(m, n - 1, cache, grid));
        cache[n-1][m-1] = sum + grid[n - 1][m - 1] + 1;
        return cache[n-1][m-1] - 1;
    }
}
// 1ms

2.递推代码

如果想要使用递推，我们还需要考虑枚举状态的顺序，这里可以从向往下枚举，从左往右枚举，因为一个更新一个状态，需要它右侧与它上边状态的答案，如此枚举可以保证一个状态在被更新时，他需要的状态已经被更新完毕了。而决策也相对更难考虑，在递推中做不到像搜索那样，搜不下去就是边界，我们需要人为地将第 0 行与第 0 列的元素都都作为决策边界。

class Solution {
    public int minPathSum(int[][] grid) {
    	int n = grid.length, m = grid[0].length;
        int dp[][] = new int[n][m];

        // 决策边界
        dp[0][0] = grid[0][0];
        for (int i = 1; i < n; i++) dp[i][0] = dp[i - 1][0] + grid[i][0];
        for (int j = 1; j < m; j++) dp[0][j] = dp[0][j - 1] + grid[0][j];

        // 状态转移
        for (int i = 1; i < n; i++){
            for (int j = 1; j < m; j++){
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }

        return dp[n - 1][m - 1];
    }
}

7.总结

• 动态规划以状态表示为核心，需要确定转移方程与边界情况
• 满足三条基本性质：最优子结构、无后效性、子问题重叠
• 解决最值、计数、存在性判定三类问题
• 使用记忆化搜索或递推地方式实现

8.Q&A

Q1：如何提升动态规划能力？ A1：两个办法：练习与积累。(a) 多做题，锻炼用状态描述问题，转移解决问题地思维。(b) 通过了解经典的动态规划类型，积累状态表示与转移的经验。

Q2：动态规划边界情况总是弄不清楚怎么办？ A2：(a) 想清楚了再写代码 (b) 用记忆化搜索的实现方式 (c) 强迫自己在纸上写出一些内容

原文: HTTPS://WNJXYK.KEJI.MOE/ALGORITHM/ALGORITHM-ABC-DYNAMIC-PROGRAMMING-INTRODUCTION/